مقاربات فنية وحضارية

لاتحظى حضارات وادي الرافدين للأسف بنفس القدر من التقدير عالميا كالحضارة المصرية واليونانية، علما أن ماقدمته هذه الحضارات للبشرية من اختراعات كالكتابة والأعداد والرياضيات والدولاب والمنشار والرمح والتقويم والحرث والزراعة والري والنقود والبيرة وغيرها تضاهي كثيرا ماقدمته الحضارات القديمة الأخرى. ولكن عددا من علماء الآثار والحوسبة أولى اهتماما كبيرا بنشأة الرياضيات والحوسبة على يد السومريين والبابلين حيث ولدت الأرقام والحوسبة اليدوية على أيدي العراقيين القدماء الذين أنشأوا اولى الحضارات البشرية في حضارات وادي الرافدين. كان سكان الحضارة الأولى المعروفة في سومر (حوالي 5000 سنة قبل الميلاد) أول من احتفظ بسجلات المعاملات التجارية على الواح الطين المفخور. وفي الواقع قد يكون المحاسب السومري الذي عاش في الجزء الأسفل من بلاد وادي ما بين النهرين حوالي 3200 قبل الميلاد أول إنسان يقوم بتسجيل الأرقام كوسيلة للتخزين، حيث استخدم النظام الرقمي الستيني الذي يستند إلى القواعد 6 و10. لقد جلب اكتشاف الحساب الفوائد الملموسة للحضارة السومرية بما في ذلك القدرة على تحديد منتجات اقتصادهم عدديا، وساهم في نمو تجارة بلاد ما بين النهرين، وأستفادت الحضارات الأخرى من ذلك لاحقا.

النظم الرقمية

بدأت المفاهيم الأساسية للأرقام في الظهور عندما أرسخت أول حضارة في العالم وهي الحضارة السومرية جذورها في بلاد ما بين النهرين منذ اكثر من 5000 سنة. واستخدم النظام الرقمي هذا خاصية الموضعية لأول مرة (اي أن قيمة الرمز المستعمل تعتمد على موضعه في الرقم). وكان للسومريين تشكيلة معقدة من النظم العددية وكان لكل مدينة طريقتها المحلية الخاصة في كتابة الارقام . في مدينة اوروك، حوالي 3100 قبل الميلاد، كان هناك أكثر من عشرة أنظمة رقمية مختلفة، فعلى سبيل المثال استُخدم نظام ارقام لحساب أشياء مختلفة مثل الحيوانات، والأدوات، والحاويات. وكان هناك نظام مختلف لحساب الجبن ومنتجات الحبوب . وتم استخدام نظام آخر لحساب كميات الحبوب وآخر لمكونات البيرة وآخر للأوزان وآخرلمناطق اليابسة وللوحدات الزمنية ووحدات التقويم، وتغيرت هذه الأنظمة على مر السنين. وتغيرت الأرقام لحساب كميات الحبوب كلما تغير حجم السلال. كان الناس يتعاملون بكميات من الحبوب كل يوم واستخدموا مهاراتهم الحسابية لحساب غيرها من الأمور التي كانت غير ذات صلة بقياسات الحجم. اخترع السومريون الحساب وبضمنه الضرب والقسمة وكانت جداول الضرب تكتب على الألواح الطينية بالقلم المدور .

وقد تطورت هذه الرموز في نظم معقدة من الأرقام حوالي 3000 قبل الميلاد، لتكون قادرة على تسجيل كميات كبيرة جدا من البضائع. ويستخدم الكاتب مجموعات مختلفة من الرموز لتسجيل كميات الأغنام أو الحبوب. ومن المعروف أن أكثر من دزينة من مختلف هذه الأنظمة كانت موجودة. ولم يكن هناك أي قاعدة موحدة، تماما كما في الوقت الحاضر حيث لا يوجد لدينا أي قاعدة موحدة لجميع الوحدات المختلفة من الأوزان والمقاييس خارج النظام المتري .

في ذلك الوقت، وضع السومريون نظم أرقام فريدة من نوعها، وذلك باستخدام قاعدة الستين بالمصطلحات العلمية، ويسمى هذا النظام الستيني (sexagesimal). كانت قاعدة النظام 60، بينما قاعدة العشرة هو ما نستخدمه اليوم. عد السومريون الأشياء مع ستين كوحدة واحدة، كان لديهم نفس الرمز للأعداد 1 و60. وللتعبير عن 70، عبروا عنها حرفيا كمجموع 60 وو10. وبالمثل، عبروا عن 125 كمجموع وحدتين من 60 ووحدة واحدة من 5. استخدم السومريون الأرقام الستينية ليس فقط لأن الرقم 60 يحتوي على العديد من القواسم أو أنه قابل للعد على أصابع كلتا اليدين ولكن لأن 60 هو المضاعف المشترك الأقل لعدد أصابع كلتا اليدين وعدد الأشهر في السنة. استخدم السومريون مفاصل أصابعهم لحساب النظام الاثني عشري (12)، وقسموا اليوم، من شروق الشمس إلى غروبها، إلى 12 جزءًا، لذلك تم تقسيم الليل والنهار معًا إلى 24 جزءًا.

طور البابليون الكتابة المسمارية على أساس المسمارية أو " شكل إسفين ". كتبوا هذه الرموز على ألواح الطين الرطب التي كانت تخبز في الشمس الحارقة. ولا تزال عدة آلاف من هذه الأقراص موجودة اليوم في المتاحف داخل وخارج العراق. واستخدم البابليون الإسفين لبصم الرموز على الطين لأنه لا يمكن استعمال الخطوط المنحنية بسهولة.

وبين 2700 ق و2000 قبل الميلاد، تم استبدال القلم المدور تدريجيا بقلم القصب الذي استخدم لضغط إسفين يشكل علامات مسمارية في الطين، لتمثيل الأرقام التي سبق ان تم تمثيل رموزها بالقلم المدور. وكانت الأرقام المسمارية القديمة غامضة لأنها تمثل مختلف النظم الرقمية التي تختلف اعتمادا على ما كان يجري فرزها. وفي حوالي 2100 قبل الميلاد في سومر، تلاقت هذه الأنظمة تدريجيا على رقم النظام الستيني المشترك الذي كان نظام مكان القيمة التي تتكون من علامات اثنين فقط، الإسفين الرأسي والأفقي، والتي يمكن أيضا أن تمثل الكسور. وقد تم تطوير هذا النظام الستيني بالكامل في بداية فترة بابل القديمة (حوالي عام 1950 قبل الميلاد)، وأصبح المعيار في بابل .

وكانت أرقام النظام الستيني التي احتفظت بقاعدة 10 وقاعدة 6 بالتناوب في سلسلة من الرموز المسمارية (الأسافين) الرأسية والافقية، وهي واحدة من أقدم أنظمة الترقيم. الرياضيات الأولى يمكن أن تعزى أيضا إلى بلاد بابل القديمة وذلك خلال الألفية الثالثة قبل الميلاد حيث كانت الجداول الإنجاز الأكثر تميزا للبابليين والتي ساعدتهم في حل المشاكل. وأصبح النظام الستيني النظام المستخدم على نطاق واسع في التجارة، ولكن تم استخدامه أيضا في الحسابات الفلكية وغيرها. وتم تصدير هذا النظام من بابل الى جميع أنحاء بلاد ما بين النهرين، وكذلك إلى بلدان البحر الأبيض المتوسط التي استخدمت النظام البابلي كمعيار للقياس والعد، بما في ذلك الإغريق والرومان والمصريين. ونحن لا نزال نستخدم النظام الستيني لحساب الوقت (دقائق لكل ساعة وثواني لكل دقيقة )، والزوايا (درجة).

على مدى السنوات الخمسمائة التالية، تطورت الكتابة تدريجيا في الكتابة المسمارية وجاء ظهور الحساب جنبا إلى جنب مع ظهور الكتابة المسمارية. ولم يعد استخدام الألواح الطينية مجرد لتسجيل أعداد السلع، ولكن نجدها في تسجيل المجاميع الحسابية والحسابات.

وحتى قبل العصر البابلي القديم أي حوالي 2000 قبل الميلاد كانت هناك الرياضيات المتقدمة بالكامل. وقد تم اكتشاف الآلاف من الأقراص الرياضية والاقتصادية، التي تظهر معرفة رائعة بالحساب، والمعادلات الخطية والتربيعية، والعديد من المنشآت الهندسية والحسابية. وهناك جداول الضرب، وجداول من المساحات، والجذور التربيعية، والثوابت المشتركة. هناك قوائم من المسائل الحسابية وضعها المعلمون، والحلول التي قدموها للطلاب. في هذا الوقت كان نظام الأرقام للحساب قد استقر على النظام الستيني، أو قاعدة الستين، وكان من الأسهل بالنسبة لهم حساب الكسور.

واليوم، يستخدم لدينا نظام الأرقام العشرية ذات القاعدة عشرة، وليس ستين، باعتبارها الوحدة الأساسية، ولكن هذا لا يعني أن اختراع السومريين أصبح باليا. في واقع الأمر، فإنه لا يزال يلعب دورا حاسما في حياتنا اليومية. على سبيل المثال، هل سبق لك أن تساءلت لماذا للساعة 60 دقيقة والدقيقة لها 60 ثانية؟ هل سبق لك أن فكرت لماذا الدائرة الكاملة لها 360 درجة ؟ كما اتضح، كان هذا ما أبقى السومريين المسار من وقتهم، وكان ذلك كيف تُعرف دائرة كاملة. قسم البابليون اليوم إلى أربع وعشرين ساعة، كل ساعة إلى ستين دقيقة، والدقيقة إلى كل ستين ثانية . وقد بقى هذا الشكل من العد للوقت لأربعة آلاف سنة الى يومنا هذا.

رموز الأرقام

يبين الجدول أدناه كيف كان السومريون والبابليون يكتبون الأرقام بالكتابة المسمارية أو ألاسفينية.

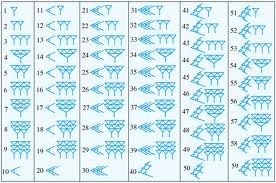
 كان أي رقم أقل من 10يمثل بأسفين يشيرإلى الأسفل.

مثال : 4

ويرمز الرقم 10 بإسفين إلى اليسار.

مثال : 20

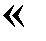
وترمز أرقام أقل من 60 عن طريق الجمع بين رموز 1 و10 .

مثال : 47

كما هو الحال مع نظام الترقيم لدينا، فأن نظام الترقيم البابلي مبني على الوحدات، أي العشرات، المئات، وألالآف المستخدمة.

مثال : 64

ومع ذلك، لم يكن لديهم رمز للصفر. عندما أرادوا التعبير عن الصفر، تركوا مجرد مساحة فارغة في العدد الذي كانوا يكتبونه . عندما يكتبون " 60"، فإنهم يضعون علامة إسفين واحدة في المركز الثاني من الأرقام .

عندما يكتبون " 120 "، فإنهم يضعوا علامتي إسفين في المركز الثاني.

فيما يلي بعض الأمثلة على أعداد أكبر .

مثال : 79883

(22*602)+(11*60)+23

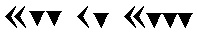
مثال : 5220062

(24*603) + (10*602) + (1*60) + 2

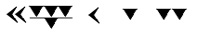
خلال السنوات الأولى من التاريخ المسجل، في بلاد ما بين النهرين القديمة جُربت طرق للحساب والقياس، وحل المشاكل الرياضية، وكانوا أول من أعطى قيمة للرقم مستندةً على مكان الرقم، والتعرف على مفهوم من الصفر (الحضارة الهندية لاحقا قدمت الصفر).

لا يبدو أن الرياضيات البابلية قد تغيرت كثيرا في السنوات 1500 التالية. قد يكون ذلك راجعا جزئيا إلى حقيقة أن لدينا عددا قليلا جدا من أقراص الرياضيات من هذه الفترة على ما يبدو . ونحن نعرف عن تطوير علم الفلك الرياضي في الفترة البابلية المتأخرة من القرون القليلة الماضية قبل الميلاد.

ونظرا لمتانة الألواح الطينية المكتوبة في بلاد ما بين النهرين، فإن الأدلة المتوفرة كبيرة، والعينات الموجودة للرياضيات تمثل جميع عصور - الممالك السومرية الرئيسية من الألفية الثالثة، الأنظمة الأكادية البابلية (الألفية الثانية)، وإمبراطوريات الآشوريين (الألفية الأولى في وقت مبكر) والفرس (القرن السادس الى الرابع قبل الميلاد)، واليونانيين (القرن الثالث قبل الميلاد إلى القرن الأول م) . كان هناك بالفعل مستوى من الكفاءة العالية في وقت مبكر من سلالة بابل القديمة، وحقبة المشرع الملك حمورابي (القرن 18 قبل الميلاد)، ولكن بعد ذلك كان هناك قليل من التقدم. ومع ذلك ازدهر تطبيق الرياضيات في علم الفلك خلال الفترات الفارسية والسلوقية ( اليونانية).

المعداد الحسابي

و وُصف المعداد الحسابي اليدوي لأول مرة في بابل وهو أول آلة حسابية فعلية معروفة لدينا، ويعتقد أنه قد اخترع من البابليين في وقت ما بين 1000 قبل الميلاد و500 قبل الميلاد. والمعداد هو جهاز يستخدم للجمع والطرح، والعمليات ذات الصلة من الضرب والقسمة. أنها لا تتطلب استخدام القلم والورق. هناك نوعان من الأشكال الأساسية للمعداد : سطح مستو خصيصا لاستخدامه مع عدادات (الجدول العد مستمر)، أو إطار مع حبات على الأسلاك.

كان المعداد الأولي بشكل يكاد يكون من المؤكد على حجر مسطح تغطيها الرمال أو الغبار. وضعت الكلمات والحروف في الرمال، وفي نهاية المطاف تم إضافة أرقام والحصى المستخدمة لمساعدة العمليات الحسابية. استخدم البابليون هذا المعداد في وقت مبكر من عام 2400 قبل الميلاد. أصل المعداد مع سلاسل هو غامض، ولكن ينظر إلى الهند، وبلاد ما بين النهرين أو مصر كنقطة محتملة للمنشأ. ولعبت الصين دورا أساسيا في تطور المعداد.

وقد وضعت مجموعة متنوعة من المعدادات؛ استندت الأكثر شعبية على نظام ثنائي خماسي، وذلك باستخدام مزيج من اثنين من القواعد (قاعدة 2 وقاعدة -5) لتمثيل الأرقام العشرية . ولكن أقرب المعدادات استخدم لأول مرة في بلاد ما بين النهرين وفيما بعد من قبل الكتبة في مصر واليونان باستخدام أرقام النظام الستيني ممثلة مع العوامل من 5، 2، 3، لكل رقم .

الرياضيات

نجح البابليون بتحقيق تقدم كبير في الرياضيات يضاهي ماحققه المصريون وحتى اليونانيين من بعدهم.

- أستخدموا الكسور العامة، وإن لم يكن كل الكسور.

- نجحوا في استخراج الجذور التربيعية للأعداد.

- تمكنوا من حل النظم الخطية.

- تعاملوا مع مثلثات فيثاغورس.

- تمكنوا من حل المعادلات التكعيبية بمساعدة الجداول.

- درسوا القياسات الدائرية.

- كانوا لا يستخدمون الصفر.

واحدة من الأقراص البابلية، (بليمبتون 322)، والتي يرجع تاريخها إلى ما بين عامي 1900 و1600 قبل الميلاد، تحتوي على جداول فيثاغورس وتظهر المعادلة

A2 + B2 = C2

موجودة حاليا في المتحف البريطاني. وعرف من علماء الرياضيات في بابل كيدينو وريماني اللذان عاشا حوالي 480- 490 قبل الميلاد.

ويبين عالم الحوسبة المشهور دونالد كنوث في بحث فريد (3) أن البابليين لم يطوروا الرياضيات فحسب بل كانوا أول من وضع لبنات الخوارزميات لتوصيف الخطوات اللازمة لحل المسائل الرياضية. ولم يتحدد علماء الرياضيات البابليين بعمليات الجمع والطرح والضرب والقسمة فحسب، فقد كانوا بارعين في حل العديد من أنواع المعادلات الجبرية، غير أنهم لم يكن لديهم منهج الجبر الذي نعرفه اليوم فكانوا يمثلون كل معادلة بسلسلة من الخطوات، خطوة بخطوة لحلها، أي عن طريق خوارزمية لحل هذه المعادلة. في الواقع، عملوا مع "لغة الآلة" التي نعرفها اليوم مع الحواسيب لتمثيل المعادلات بدلا من لغة رمزية.

ولا يمكن أن نتكلم عن الخوارزميات من دون أن نذكر عالم الرياضيات الأسلامي محمد بن موسى الخوارزميّ الذي كتب مؤلفه الشهير: "الكتاب المختصر في حساب الجبر والمقابلة"، في حوالي 830 ميلادية بتشجيع من الخليفة العباسي المأمون، حيث قدم عرضا شاملا لحل المعادلات متعددة الحدود حتى الدرجة الثانية، وناقش الأساليب الأساسية ل"الحد" و"التوازن" في اشارة الى تبديل العوامل إلى الجانب الآخر من المعادلة. وكان انجاز الخوارزمي الحسابي المسؤول عن إدخال الأرقام العربية على أساس نظام الترقيم الهندي العربي إلى العالم الغربي.

علم المثلثات البابلي

استنبط البابليون شكلهم الفريد من علم المثلثات خلال الفترة البابلية القديمة (1900-1600 قبل الميلاد)، قبل أكثر من 1500 عام من الشكل اليوناني. من اللافت للنظر أن علم المثلثات الخاص بهم لا يحتوي على أي من السمات المميزة لعلم المثلثات الحديث لدينا - فهو لا يستخدم الزوايا ولا يستخدم التقريب.

كان لدى البابليين تصورا مختلفا تمامًا للمثلث القائم. لقد رأوا أنه نصف مستطيل، وبسبب نظام الأرقام الستيني (الأساس 60) المتطور، تمكنوا من بناء مجموعة متنوعة من المثلثات القائمة باستخدام النسب الصحيحة فقط. نحن نعلم الآن أن البابليين درسوا علم المثلثات لأن لدينا جزءًا من أحد جداولهم المثلثية.

Plimpton 322 عبارة عن لوح طيني مكسور من مدينة لارسا القديمة، والتي كانت تقع بالقرب من تل السنكيره في العراق. تمت كتابة اللوح بين 1822-1762 قبل الميلاد. في عشرينيات القرن الماضي، باع عالم الآثار والأكاديمي والمغامر إدغار جيه بانكس اللوح للناشر الأمريكي وفاعل الخير جورج آرثر بليمبتون. ترك بليمبتون مجموعته الكاملة من اللوحات الرياضية إلى جامعة كولومبيا في عام 1936، وهي موجودة هناك اليوم في مكتبة الكتب والمخطوطات النادرة. إنه متاح عبر الإنترنت من خلال مبادرة المكتبة الرقمية المسمارية.

في عام 1945، تم الكشف عن أن اللوح يحتوي على سلسلة معقدة للغاية من الأرقام الصحيحة التي تلبي معادلة فيثاغورس، والمعروفة باسم ثلاثية فيثاغورس. هذه هي العلاقة الأساسية بين الجوانب الثلاثة للمثلث القائم الزاوية، وقد أثبت هذا الاكتشاف أن البابليين كانوا يعرفون هذه العلاقة قبل أكثر من 1000 عام من ولادة عالم الرياضيات اليوناني فيثاغورس.

المعاملات التجارية

ان بلاد ما بين النهرين القديمة لم يكن لديها اقتصاد العملة، لذلك وضعت نظاما موحدا للأوزان لتنفيذ العديد من المعاملات التجارية الخاصة بهم. وكانت أصغر وحدة هي الوزن التقريبي لحبة واحدة من الشعير.

الشكل المدرج إلى الأسفل هو وثيقة تسجيل بيع قطع من الأرض، وربما لمشتر واحد. ويسمى مثل هذا السجل " Kudurru ". الأعمدة التسعة من النص المكتوب على كل من الوجه (الصورة العليا) والقفاء (الصورة أسفل) وصف لصفقة البيع بقدر كبير من التفصيل. على الرغم من أنها على شكل قرص من الطين، فأنها مصنوعة من الحجر مما يدل على أن هذه الوثيقة كانت تعتبر مهمة جدا لأن الحجر سلعة نادرة وباهظة الثمن في بلاد ما بين النهرين، حتى يكون سجلا دائما وغير قابل للتدمير. تم الاحتفاظ بسجلات المبيعات هذه في المعابد لمنحها حماية الآلهة، في نفس الوقت جعلها في متناول التدقيق العام. يسجل في الوثيقة مجالات الحقول المكتسبة وكميات الفضة والسلع الأخرى المستخدمة لشراء الأرض. شملت هذه السلع دهون الأغنام والصوف والخبز.

 زيد حبه

........................

المصادر:

1- “The Sumerians, Their History, Culture, and Character”, by Samuel Noah Kramer, The University of Chicago Press, 1963

2- “Ancient Babylonian Algorithms”, Donald E. Knuth, Stanford University, Communications of the ACM, July 1972

3- “Pathfinders-The Golden Age of Arabic Science”, Jim Al-Khalili, Penguin Books, 2010.

4- “Plimpton 322 is Babylonian exact sexagesimal trigonometry”

Daniel F.Mansfield, N.J.Wildberger

Historia Mathematica, Volume 44, Issue 4, November 2017, Pages 395-419

5- Babylonian Mathematics

http://www.math.tamu.edu/~dallen/masters/egypt_babylon/babylon.pdf