علوم

هل هي حدث فريد أم متكرر إلى مالانهاية؟ ماذا قبل وماذا بعد البغ بانغ؟

صراع النسبية العامة وميكانيكا الكموم الكوانتوم وما بعدهما، هل سنصل يوماً لنظرية كل شيء، وهل نعيش في كون متعدد؟ (النماذج المختلفة لأكوان متعددة) وهل نعيش في محاكاة حاسوبية، كون "ماتريكس"؟

أ‌- مبدأ التكافؤ والجاذبية النسبية:

فشلت نظرية النسبية، كما صاغها أينشتاين عام 1905، بسبب سهوين:

- لم يقل شيئًا عن الكيفية التي يرى بها المراقبون المتسارعون العالم وقوانين الفيزياء.

- لم يشمل الجاذبية في جميع النظريات الفيزيائية الموصوفة بواسطة قوانين مستقلة عن المراقب والقصور الذاتي.

ولكن، كما لاحظ أينشتاين، كان "التسارع" و"الجاذبية" هما أيضًا كلمتان رئيسيتان لظاهرة لوحظتا تجريبياً وذكرا عدة مرات هنا: عالمية السقوط الحر للأجسام. كان أينشتاين أحد أتباع التجارب الفكرية 1 (Gedankenexperiment باللغة الألمانية)، لذلك حاول أن يتخيل ما قد يراه مراقب في السقوط الحر في مجال الجاذبية، والذي وصفه لاحقًا بأنه "أسعد فكرة لوجوده" الأمر الذي دفعه إلى اكتشاف مبدأه الأساسي وهو، مبدأ التكافؤ. في الواقع، تخيل أينشتاين نفسه منعزلًا في مصعد يسقط بحرية دون إمكانية مراقبة البيئة الخارجية، أدرك أن أيا من التجارب الميكانيكية التي يمكنه القيام بها لن يمنعه من الاعتقاد بأنه يعاني من القصور الذاتي وبعيدًا عن أي مصدر. من الجاذبية. ومع ذلك، كان هذا صحيحًا فقط بسبب المساواة، لجميع الأشياء، بين سقوط الأجسام ذات الكتل والأجسام ذات الكتل الخاملة. تشير هذه المساواة ضمنيًا إلى أنه إذا رمى شيئًا أمامه مباشرة، فسوف يراه يستمر في مسار مستقيم، حتى لو كان أي مراقب ثابت في مجال الجاذبية سيرى المصعد ومحتوياته تسقط مع تسارع مماثل. وعلى العكس من ذلك، إذا افترض المرء أن المصعد يقع بعيدًا عن أي مصدر لحقل الجاذبية ويتم سحبه بتسارع ثابت، فيمكن لمراقب مقفل في هذا "الإطار المرجعي المتسارع" أن يعتقد تمامًا أنه يقع في مجال الجاذبية ولن يكون لديه وسيلة ميكانيكية لتمييز تسارع مرتبط بفعل قوة شد عن ذلك المرتبط بمجال الجاذبية.

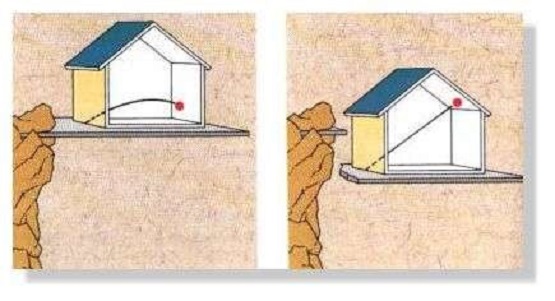
أعلاه، توضيح لمبدأ التكافؤ بين الكتل الجادة والخاملة. أدناه، رسم توضيحي للقصور الذاتي الظاهر، من وجهة نظر المراقب في السقوط الحر (المرتبط بالمنزل)، لمسار جسم تم إطلاقه في مجال الجاذبية.

كان من الممكن صياغة كل ما سبق في وقت مبكر من عصر نيوتن، ومع ذلك، كانت عبقرية أينشتاين هي النظر في كل هذه الأشياء من وجهة نظر جديدة، والتأكيد على أن المعنى الحقيقي للملاحظة المعروفة لم تكن عالمية السقوط الحر هوية الكتل الجادة والخاملة، بل هوية الجاذبية والتسارع: التغيير المناسب للإطار المرجعي يمكن دائمًا على ما يبدو أن يقمع تأثير مجال الجاذبية. ومع ذلك، لا يمكن أن يكون هذا المبدأ صحيحًا إلا محليًا، نظرًا لأن المجال الحقيقي، مثل مجال الجاذبية الأرضية، ليس ثابتًا، مما يعني، وجو انحراف بين مسارات جسمين على مسافة كافية. في السقوط الحر (نتحدث عن "تأثير المد والجزر" أو "الانحراف الجيوديسي").

رسم توضيحي للاختلاف بين التسارع المنتظم (على اليسار) ومجال الجاذبية الحقيقي (على اليمين)، عندما ينظر المرء ليس فقط إلى الفعل المحلي، ولكن في مجال أكبر. يدفع تأثير المد والجزر الكتل النقطية لتقترب ببطء من بعضها البعض.

وهكذا عقد أينشتاين أول عنصرين رئيسيين في "النسبية العامة" المستقبلية:

- لكي يتعامل مبدأ النسبية أيضًا مع الأطر المرجعية المتسارعة، كان لا مفر من التركيز على الجاذبية؛

- بما أن الجاذبية والتسارع لا يستطيعان، بالمعنى الدقيق للكلمة، تعويض بعضهما البعض محليًا، فإن النسبية العامة لا بد أن تكون نظرية محلية، والتي بدت متماسكة مع فعل الجاذبية الذي لا يحدث "على مسافة"، ولكن "بواسطة اتصال". علاوة على ذلك، نظرًا لأن إعادة صياغته لمبدأ النسبية قد تضمنت تضمين الكهرومغناطيسية في النظريات النسبية، فسرعان ما كان لدى أينشتاين حدس مفاده أن الضوء يجب أن يتأثر أيضًا بمجال الجاذبية. في الواقع، إذا تخيل المرء نفسه، في مصعد في حالة سقوط حر، مصدر ضوء يُصدر فجأة شعاعًا ضوئيًا، فهناك احتمالان. إما أن يلاحظ المراقب الموجود في المصعد أن الضوء يتبع مسارًا مستقيمًا، وهذا يعني أنه بالنسبة لمراقب على سطح الأرض، فإن المسار الذي يتبعه الضوء ليس مستقيمًا؛ أو أن المراقب في المصعد نفسه يلاحظ أن مسار الضوء ليس مستقيمًا، في حين أنه يبدو كذلك بالنسبة للمراقب على الأرض. ومع ذلك، بالنسبة لأينشتاين، ليس هناك أي تردد في أن يكون لديك: لا يمكن للمراقب على الأرض بأي حال من الأحوال أن يصدق نفسه بالقصور الذاتي لأنه مضغوط على الأرض في مجال الجاذبية، بينما من ناحية أخرى، المراقب في حالة سقوط حر يمكن أن يعتقد محليا أنه في حالة قصور ذاتي. وبالتالي، يبدو منطقيًا أن الضوء ينتقل في خط مستقيم بالنسبة للمصعد، مما يعني أيضًا أنه يجب أن يتأثر بمجال الجاذبية، مثل أي جسم مادي 2. لاحظ أيضًا أن هذا يتفق مع مبدأ التكافؤ بين الكتل الخاملة والخطيرة، فقد أظهرت النسبية الخاصة أن القصور الذاتي مرتبط بالطاقة وليس فقط بالكتلة بحد ذاتها (ومع ذلك، تجدر الإشارة إلى أن الحديث عن "قصور الضوء" هو هراء لأن معيار سرعته لا يمكن أن يتغير). بناءً على قوة هذا المنطق، كتب أينشتاين في عام 1911 مقالًا توقع فيه تأثير الجاذبية على الضوء، وحيث أظهر أن هذا التأثير، بالإضافة إلى انحراف الضوء المار بالقرب من الشمس، يجب أن يكون كذلك. ترجم بواسطة "احمرار" الضوء المنبعث من جسم سماوي ضخم (نتحدث عن "تأثير أينشتاين"): تردد الضوء المرصود بعيدًا عن المصدر أقل من ذلك الذي انبعث منه عند سطح الجسم.

ومع ذلك، فإن هذه الفرضية الخاصة بالتأثير المحتمل للجاذبية على الضوء، مهمة جدًا في النسبية العامة، وهي تشهد على الاختلاف الأساسي بين وجهة نظر أينشتاين حول الجاذبية النسبية ووجهات نظر الشخصيات الأخرى.، مثل بوانكاريه Poincaré أونورستروم Nordström. في الواقع، وضع مبدأ التكافؤ في الموضع الأول من افتراضات نظريته، اختار أينشتاين، في عام 1912، التخلي عن صيغة لورنتز المتغيرة للجاذبية، من أجل إعطاء الأخيرة دورًا خاصًا فيما يتعلق بالجاذبية. - فيما يتعلق بالظواهر الفيزيائية الأخرى، وهو نهج يسمح لها أيضًا بتوسيع مبدأ النسبية ليشمل جميع المراقبين، حتى المتسارعين منهم. لذا بينما يحاول الجميع تغيير الجاذبية للتعبير عنها في الزمكان عند مينكوفسكي، يتخذ أينشتاين مسارًا مختلفًا تمامًا ويفضل تعديل مفهوم الزمكان مرة أخرى. ووفقًا لوجهة نظره، فإن عالمية الجاذبية وسقوط الأجسام الحر تجدان نفس التفسير، وهو أن الجاذبية ليست "قوة" مثل الآخرين، ولكنها مجرد تعبير عن هندسة الفضاء (-زمن). إذا كان بإمكان المراقبين في السقوط الحر أن يصدقوا أنفسهم بالقصور الذاتي، فذلك لأنهم كذلك، تمامًا مثل مراقبي لورنتزيان في غياب مجال الجاذبية. ببساطة، عندما يوجد مصدر لحقل الجاذبية، يتم تعديل الهندسة الزمكانية، ولا يجب اعتبار الفضاء (الزمن) إقليديًا (أو مسطحًا)، بل منحنيًا (أو ريمانيان). علاوة على ذلك، نظرًا لأنه كان معروفًا منذ مينكوفسكي أن المكان والزمان مجرد أوهام، وأن الكائن المطلق "الحقيقي" هو الزمكان المينكوفيسكس Minkowskian ، فقد جاء أينشتاين بشكل أكثر دقة للتخلي عن الهندسة المينكوفسكية Minkowskian. لاعتماد هندسة ريمانية زائفة تجعل من الممكن وصف زمكان منحني.

في هذا النهج، فإن حقيقة أن المسارات التي يتبعها المراقبون "في السقوط الحر" (أي كل تلك التي لا تخضع لأي قوة حقيقية) لم تعد خطوطًا مستقيمة، ولكن مسارات أخرى، تجد تفسير طبيعي. هذه المسارات، التي تعمم فكرة "الخط الإقليدي"، تعتمد فقط على الهندسة وليس على طبيعة الراصد "الذي يسقط". ونظرًا لأن الضوء، مثل أي جسم مادي آخر، مدرج أيضًا في الزمكان، فمن الحتمي أن يتأثر أيضًا بمجال الجاذبية، حتى لو كانت الكتلة الصفرية للفوتون تشير إلى أن خطوط الأكوان المتعقبة ليست مثل تلك الخاصة بالجسيمات الضخمة. النسبية العامة كونها هندسية للجاذبية عبر هندسة ريمان، يصبح من الحتمي، من أجل فهم جوهر نظرية أينشتاين بشكل أفضل، قول بضع كلمات عن هذه الهندسة، بوضوح دون الخوض في التفاصيل بالضرورة.

ب - الهندسة الريمانية والجيوديسية:

الهندسة التي تم دراستها من المدرسة الابتدائية، والمستخدمة يوميًا، هي الهندسة إقليدس، عالم الرياضيات اليوناني من القرن الرابع قبل الميلاد. يحدد الأخير بدقة المفاهيم المألوفة للمستوى، والخط، والنقطة، وما إلى ذلك، وإضفاء الطابع الرسمي على نظريته بالكامل في عناصره، مقسمة إلى 13 كتابًا، والتي تبدأ بتعريفات مختلفة و5 افتراضات أساسية. ومع ذلك، من بين هذه الافتراضات، هناك واحد تسبب في تدفق الكثير من الحبر، المعروف باسم "المسلمة الخامسة لإقليدس"، أو حتى "مسلمة المتوازيات". يقول إنه "في ظل وجود خط ونقطة خارجه، يوجد خط واحد فقط يمر عبر هذه النقطة الموازية للخط الأول والمضمنة في المستوى الذي يحدده الأخير النقطة التي تقع خارجه "3. في الواقع، طرح السؤال لفترة طويلة لمعرفة ما إذا كانت هذه الفرضية واحدة حقًا، أو ما إذا كان يمكن توضيحها من الآخرين وبالتالي فهي مجرد نظرية.

رسم توضيحي لافتراض إقليدس الخامس: بالنظر إلى الخط (BC) والنقطة A، لا يوجد سوى سطر واحد موازٍ لـ (BC) يمر عبر A. البيان الأولي للمسلمة يتعلق في الواقع بالقيم الزوايا (MAC) و (NAB) مقارنة بزوايا (ACB) و (ABC).

There's more to discover in the WordPr

لم تتم تسوية السؤال بشكل نهائي حتى القرن التاسع عشر بواسطة عالم الرياضيات الألماني كارل فريدريش غاوس، الروسي نيكولاي الأول فانوفيتش لوباتشيفسكي والمجري يانوس بولياي، اللذان قاما، بشكل مستقل عن بعضهما البعض، ببناء "أشكال هندسية منحنية" تم فيها تعديل هذا الافتراض الخامس، حيث كان عدد المتوازيات صفرًا أو حتى لانهائيًا. لكون هذه الأشكال الهندسية متماسكة تمامًا مثل تلك الخاصة بإقليدس، فإن هذه الفرضية الخامسة كانت بالفعل واحدة. ومع ذلك، قدم عالم الرياضيات الألماني جورج فريدريش برنارد ريمان مساهمة كبيرة في هذه المشكلة، عندما صاغ، بعد سنوات قليلة، ما يعرف الآن باسم "هندسة ريمان". كان الأمر يتعلق بالتعميم، على المساحات من أي أبعاد، لمفهوم الانحناء الذي قدمه غاوس Gauss، وأصبحت هندسة Gauss وBolyai وLobachevski وحتى هندسة إقليدس مجرد أمثلة معينة على "الهندسة الريمانيّة" (الفضاء الإقليدي - أو الإقليدية الزائفة مثل مساحة مينكوفسكي - هي مساحة منعدمة الانحناء). والأكثر إثارة للدهشة أنه أثناء تطوير هندسته، كان لدى ريمان حدس مفاده أنه نظرًا لأنه كان أكثر اتساعًا وعمومية من نظيره إقليدس، فقد يكون، على الرغم من المظاهر، أكثر توافقًا مع "العالم الحقيقي ".

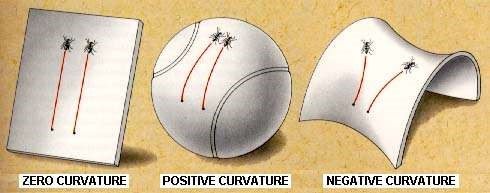
في الواقع، على الرغم من تأكيدات الفيلسوف الألماني إيمانويل كانط، فليس للفضاء سبب ليكون إقليديًا بديهيًا، لأنه حتى لو بدا أن التجارب التي أجريت تتفق مع الهندسة الإقليدية، يمكننا فقط إجراء قياسات خطوة بخطوة وعلى مسافات قصيرة. الآن، خصوصية الهندسة الإقليدية هي أنها يمكن أيضًا صياغتها بطريقة "عالمية"، وجميع الخصائص مستقلة عن مقياس القياس المستخدم. من ناحية أخرى، فإن المساحات الريمانية متطابقة محليًا مع الفضاء الإقليدي، ولكنها قد لا تكون متجانسة، أو متناحرة، أو حتى "ثابتة على نطاق واسع". هذه الملاحظة، التي قد تبدو للوهلة الأولى مجردة بعض الشيء، فهي ليست سوى نسخ لشيء معروف جيدًا من الآن فصاعدًا: حتى لو بدت الأرض مسطحة بالنسبة لنا، فنحن نعلم جيدًا أن هذا صحيح محليًا فقط، الأرض كونها سطحًا منحنيًا أقرب إلى الكرة منها إلى السطح المستوى. لذلك كان حدس ريمان بكل بساطة أن التسطيح الظاهري للفضاء ربما كان مجرد وهم مشابه لتسطيح الأرض، فقط القياسات على مسافات أكبر يمكن أن تحل هذا السؤال. وهكذا، كما فعل أينشتاين بشكل مستقل لاحقًا، أدرك ريمان أن هندسة الفضاء لا يمكن تحديدها إلا بالتجربة. توضيح لحقيقة أن الكرة (أو أي سطح منحني أملس آخر) يمكن استيعابها محليًا في سطح مستوى.

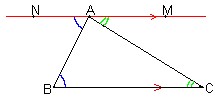
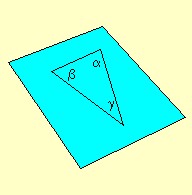
فيما يتعلق بهذا التحديد التجريبي، من المستحسن عمل قوس رياضياتي أخير حول موضوع مفهوم الانحناء. في الواقع، هناك نوعان من الانحناء: الانحناء الجوهري، والانحناء الخارجي، فقط النوع الأول "قابل للقياس تجريبيًا" ومُحدد جيدًا لكائن "مشمول" في الفضاء الذي يدرسه. بتعبير أدق، يمكن قياس الانحناء الجوهري للفضاء مباشرة باستخدام دراسة خصائص الأشكال الهندسية المضمنة في ذلك الفضاء. وهكذا، في حالة الأسطح، يمكن تحديد الانحناء الجوهري، على سبيل المثال، من خلال دراسة المثلثات التي يمكن رسمها على هذا السطح، ومجموع زوايا المثلث يساوي 180 درجة فقط في حالة سطح مستو (انظر الشكل التالي).

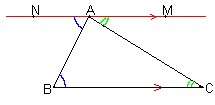رسم توضيحي لتحديد علامة الانحناء الجوهري للسطح باستخدام مثلث مرسوم عليه. إذا كان السطح مسطحًا (= إقليدي)، فسيكون مجموع زوايا المثلث دائمًا يساوي 180 درجة. من ناحية أخرى، إذا كان الانحناء موجبًا (الشكل المركزي)، فسيكون هذا المجموع أكبر، أو أصغر إذا كان الانحناء سلبيًا (الشكل السفلي). نلاحظ أن جوانب المثلث بحكم التعريف هي "جيوديسية" (انظر لاحقًا في النص)، التعميم للمساحات المنحنية لمفهوم الخط الإقليدي المستقيم.

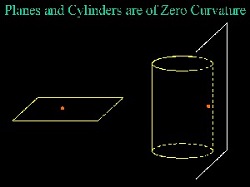
هناك طريقة أخرى لتحديد علامة الانحناء الجوهري وهي النظر، عند نقطة معينة، في المستوى المماس للسطح وإلقاء نظرة على سلوك السطح فيما يتعلق بهذا المستوى المماس، حول النقطة التي تم النظر فيها. إذا كان السطح لا يلمس المستوى وظل موجودًا على نفس الجانب (حالة الكرة)، يكون الانحناء موجبًا. إذا اعترض السطح الطائرة وعبرها حتى (حالة "سرج الحصان")، يكون الانحناء سالبًا. أخيرًا، إذا كان السطح يحتوي على خط تقاطع مع المستوى، ولكنه لا يتقاطع معه، فإن الانحناء يكون صفراً (حالة المستوى أو الأسطوانة، انظر الشكل التالي)

الانحناء الخارجي هو، من جانبه، كمية لا يتم تعريفها إلا عندما يعتبر المرء الفضاء الهندسي جزءًا من مساحة ذات أبعاد أعلى. هذا على سبيل المثال ما نفعله عندما نعتبر السطح داخليًا إعادة إلى فضاء ثلاثي الأبعاد. وبالتالي، يمكننا أن نعتقد مسبقًا أن الأسطوانة عبارة عن سطح منحني، ومع ذلك، إذا رسمنا مثلثًا على سطح أسطوانة، يمكننا بسهولة أن نرى أن مجموع هذه الزوايا الثلاث هو بالفعل 180 درجة: الأسطوانة لا لديه انحناء خارجي واحد فقط (انظر الشكل التالي). هناك طريقة أخرى لفهم هذه النتيجة وهي الاعتقاد بأن الأسطوانة ليست أكثر من "مستوى ملفوف"، وطالما أنه يمكن "فتح" سطح ووضعه مسطحًا بدون المسيل للدموع، فهذا يعني أنه ليس منحنيًا بطبيعته. وهي مجرد طريقة معقدة لقول إنه من المستحيل عمل نمط كروي بورقة واحدة دون الحاجة لاحقًا إلى قطع جزء من الورقة للحصول على الكرة.

التكافؤ الجوهري بين الطارة والمستوى الإقليدي. حتى إذا تم اعتباره كسطح مغمور في مساحة ذات بعد أعلى، فإن الطارة لها انحناء خارجي، فإن هذا لا يميزها حقًا لأنه يتم تعريفها بطريقة فريدة فقط بمجرد إعطاء "التضمين".

كان هذا الاستطراد في الانحناءين مهمًا، لأنه يسمح لنا بالإصرار على حقيقة أن الانحناء الوحيد الذي تم ذكره لاحقًا سيكون الانحناء الجوهري، وهو الحجم، بطريقة ما، "مطلق" وبالتالي يمكن تحديده تجريبيًا.. بتعبير أدق، يفترض أينشتاين، في نظريته عن النسبية العامة، أن الزمكان هو فضاء ريماني، وأن انحراف المسارات بين المراقبين في السقوط الحر في مجال الجاذبية ليس سوى "دليل رصد" للانحناء الجوهري الناجم عن مصدر المجال. بعبارة أخرى، وفقًا لأينشتاين، إذا كان بإمكان المراقبين في السقوط الحر في مجال الجاذبية أن يدّعوا محليًا أنهم قصور ذاتي، فذلك لأنهم حقًا: المراقبون بالقصور الذاتي هم أولئك الذين يسقطون سقوط حرًا، وهذا يعني - الأجسام التي لا تتعرض لأية قوة غير الجاذبية. ومع ذلك، فإن تأثير الجاذبية (= الانحناء الجوهري للزمكان)، يمكن فقط "محوه بتغيير الإحداثيات" محليًا، ويبقى أثر الانحناء عندما يكون مهتم بالفيزياء، أو في مسارات المراقبين بالقصور الذاتي، عبر مجالات ممتدة. بدلاً من اتباع "الخطوط المستقيمة"، كما كان الحال في النسبية الخاصة، يتبع المراقبون بالقصور الذاتي للنسبية العامة الجيوديسية، وهي منحنيات مكافئة محليًا للخطوط المستقيمة وتعممها في إطار الهندسة الريمانية.

في الواقع، فإن فكرة الخط المستقيم التي ذكرها إقليدس هي فكرة الخط الذي يتطابق مع نفسه في جميع النقاط، ومع ذلك، هناك تعريف آخر محتمل ألا وهو القول بأن الخط المستقيم هو أقصر طريق يربط بين نقطتين معينتين. وهكذا، يمكن للمرء أن يوسع هذا التعريف الأخير ليشمل حالة المساحات المنحنية (= الريمانيةriemannians)، حيث يتم البناء العالمي للمنحنى خطوة بخطوة، حتى يتم إعطاء الجيوديسية. كما تستخدم الجيوديسيا باعتبارها تعميمات طبيعية للخطوط المستقيمة على نطاق واسع كائنات رياضياتية. على سبيل المثال، عندما نسير للأمام مباشرة، فإن الأرض ليست مسطحة بل منحنية، فنحن لا نتبع خطًا مستقيمًا، بل خطًا جيوديسيًا: من خلال الاستمرار بشكل كافٍ نجد أنفسنا عند نقطة البداية. وحقيقة أن هذه المسارات هي الأقصر فهي أيضًا مهمة جدًا للملاحة الجوية أو البحرية، ولهذا السبب تقترب الطائرات التي تعبر المحيط الأطلسي من القطب الشمالي، بينما يبدو على الخريطة أنها تطول المسافة. ترتبط هذه النقطة الأخيرة أيضًا بالاستحالة (المذكورة أعلاه) من صنع نمط كروي ذي صفيحة مسطحة، وهي مشكلة ستظهر لاحقًا عند وصف سقوط جسيم في ثقب أسود. ومع ذلك، قبل الوصول إلى وصف هذه "الأشياء" التي تنبأت النسبية العامة بوجودها، يبقى من الضروري إنهاء وصف النسبية العامة باختصار، والطريقة التي ينتهي بها أينشتاين إلى اكتشافها وما هي أولى اختباراتها التجريبية.

رسم توضيحي، من خلال الانحراف الذي يظهر بين اثنين من الجيوديسيا الممتدة بشكل كافٍ، للأنواع الثلاثة المحتملة للانحناء لسطح ريماني (= مساحة ثنائية الأبعاد) مكافئ محليًا للمستوى الإقليدي. الفضاء الأول هو الفضاء الإقليدي نفسه، مسطح في كل مكان؛ الثاني يشبه سطح الأرض، مع انحناء إيجابي، والأخير له انحناء سلبي، كما هو الحال بالنسبة لهندستي بولاي ولوباتيفسكي Bolyai و Lobachevski. رسومات للمقارنة مع الشكل السابق توضح تأثير المد والجزر. المصدر "رحلة إلى الجاذبية والزمكان" بقلم ج.أ.ويلر ، مكتبة Scientific American.

ثورة النسبية العامة أو عندما أعاد أينشتاين رسم أشكال الكون

S² = c² (t2-t1)² - (x2-x1)²,

ds² = c² dt² - dx²,

ds² = gtt dt² + gxx dx² + 2 gtx dx dt,

المكان والزمان عند أينشتاين، مرتبطان ارتباطًا وثيقًا. باكتشاف النسبية الخاصة عام 1905، أزعج أينشتاين كل مفاهيم الفيزياء الكلاسيكية. بعد عشر سنوات، مع النسبية العامة، أعاد رسم أشكال الكون ذاتها ورسم له هيكيلية أخرى مغايرة. منذ ذلك الحين، استمر التحقق من صحة حدسه اللامع من خلال الظواهر الكونية مثل الثقوب السوداء أو موجات الجاذبية. توقع أينشتاين في نظريته عن النسبية العامة، أن وجود الثقوب السوداء لن يتم إثباته حتى السبعينيات. هذه الأجسام ضخمة جدًا لدرجة أنها يمكن أن تشوه الزمكان بشكل لا نهائي ... أو حتى تمزقه. في 14 مارس 1879، عندما ولد ألبرت أينشتاين في أولم بألمانيا، كانت العلوم الفيزيائية صرحًا يقوم على ركيزتين. من ناحية أخرى، فإن قوانين الحركة (أو الكينماتيكا) للأجسام المادية، التي ذكرها غاليليو، وقوانين الجاذبية الكونية لنيوتن متقنة تمامًا تقريبًا. من ناحية أخرى، فإن الكهرومغناطيسية - مع البحث عن التيارات الكهربائية والمجالات المغناطيسية والضوء - تسير على قدم وساق: تم جمع القوانين التي تحكمها في نظرية بواسطة الفيزيائيين جيمس ماكسويل (1831-1879) وهندريك لورنتز (1853-1928). العقل والحتمية والعلم ينتصرون! هذا هو قرن التجارب: الأدوات متقنة، دقة القياسات محسوسة ... وهنا تبرز أسئلة جديدة.

السؤال الأول، الأكثر تعقيدًا بلا شك، هو سرعة الضوء. منذ غاليليو، نعلم أن سرعات الأجسام المتحركة تتزايد. من الناحية النظرية، يجب أن يكون هذا هو الحال أيضًا بالنسبة للضوء. ضع مصباحًا على رأس الصاروخ: يجب أن تكون سرعة شعاع الضوء مساوية لمجموع سرعات الصاروخ والضوء. لايهم، هذه ليست القضية. إنه يساوي الضوء وحده. الفيزيائيان الأمريكيان ألبرت ميكلسون وإدوارد مورلي، اللذان طورا في عام 1887 تجربة معقدة تهدف إلى التحقق من أن سرعة الأرض تضاف إلى سرعة الضوء على حسابهما ... ولكن لا يوجد شك حتى الآن لمهاجمة العقيدة الجليلة وجها لوجه التي تقول بثبات سرعة الضوء في كافة الأحوال.

السؤال الثاني يتعلق بالزئبق. في منتصف القرن التاسع عشر، لاحظ العديد من علماء الفلك بالفعل تحولًا طفيفًا في الحضيض الشمسي (نقطة مداره الأقرب إلى الشمس) مقارنة بتنبؤات نظرية نيوتن، ومع ذلك فهي فعالة جدًا في حساب موقع الكواكب: تقدم بنحو 43 ثانية زاوية في القرن. تم ابتكار حلول مخصصة: نحاول تعديل قانون نيوتن للجاذبية، ونفترض وجود كوكب لم يكتشف من قبل، فولكان ، يدور بين الشمس وعطارد ، والذي من شأنه أن يزعج مجال جاذبيته هذا الأخير ويشرح التأخر الملحوظ ... ومع ذلك، لا يمكّن لأي من هذه المقترحات من حل المشكلة بشكل صحيح.

كانت هذه هي حالة العالم العلمي في عام 1905 عندما نشر أينشتاين الشاب، الذي لم يكن قد أكمل درجة الدكتوراه، خمس أوراق بحثية أساسية.

فبدلاً من التبريد، ربما يكون الكون في الواقع يسخن نتيجة لانهيار الجاذبية للمادة المظلمة والغاز.

"يوفر قياسنا الجديد تأكيدًا مباشرًا للعمل الأساسي لجيم بيبلز - الحائز على جائزة نوبل في الفيزياء لعام 2019 - الذي وضع النظرية حول كيفية تشكل الهياكل واسعة النطاق في الكون. مع تطور الكون، تسحب الجاذبية المادة المظلمة والغاز إلى المجرات والعناقيد المجرية. هذا الانجذاب عنيف جداً لدرجة أنه يتم ضغط المزيد والمزيد من الغازات وتسخينها، "يشرح عالم الكونيات في جامعة ولاية أوهايو يي-كوان تشيانغ ذلك.

كون بدائي أبرد من الكون الحالي:

لقياس التغيرات الحرارية على مدى العشرة مليارات سنة الماضية، قام تشيانغ وزملاؤه بدمج البيانات من القمر الصناعي الفلكي بلانك الذي يعمل بالأشعة تحت الحمراء التابع لوكالة الفضاء الأوروبية ومسح سلون الرقمي للسماء (SDSS). في حين أن بلانك كانت أول مهمة أوروبية لقياس درجة حرارة الخلفية الكونية المنتشرة (CMB)، فإن SDSS هي دراسة ضخمة متعددة الأطياف خلقت أكثر الخرائط ثلاثية الأبعاد تفصيلاً للكون.

الخلفية الكونية المنتشرة التي لاحظتها بعثة بلانك على ترددات مختلفة. ائتمانات: تعاون بلانك

من مجموعات البيانات هذه، عبر الفريق ثمانية من خرائط كثافة السماء بلانك مع 2 مليون مرجع طيفي للانزياح الأحمر SDSS. بدمج قياسات الانزياح الأحمر (التي تُستخدم عادةً لتحديد مدى سرعة تحرك الأجسام بعيدًا عنا) وتقديرات درجة الحرارة المستندة إلى الضوء، قارن الفريق درجة حرارة سحب الغاز البعيدة (في الوقت المناسب) مع تلك الأقرب إلى الأرض.

من هناك، تمكن فريق البحث من تأكيد أن متوسط درجة حرارة الغاز في بدايات الكون (حوالي 4 مليارات سنة بعد الانفجار العظيم) كان أقل مما هو عليه الآن. يبدو أن هذا يرجع إلى الانهيار الثقالي للبنية الكونية بمرور الوقت، وهو اتجاه سيستمر ويصبح أكثر كثافة مع استمرار تسارع توسع الكون.

تم استخدام بيانات SDSS لإعادة بناء خرائط ثلاثية الأبعاد لمناطق الكون مع مئات الآلاف من المجرات. الائتمان: SDSS

كما لخصها تشيانغ، فإن الكون يسخن بسبب العملية الطبيعية لتشكيل المجرات والشبكة الكونية، ولا علاقة له بالتغيرات في درجة الحرارة هنا على الأرض. تحدث هذه الظواهر على مستويات مختلفة جدًا. وهي غير مرتبطة على الإطلاق بحرارة الأرض.

عواقب الاحترار التدريجي للكون:

في الماضي، جادل العديد من علماء الفلك بأن الكون سيستمر في البرودة مع تمدده، مما سيؤدي حتما إلى البرد الكبير (أو التجمد الكبير). في المقابل، أظهر تشيانغ ورفاقه أن العلماء يمكنهم تحديد تطور تكوين الهياكل الكونية من خلال "التحقق من درجة حرارة" الكون.

يمكن أن يكون لهذه النتائج أيضًا تداعيات على النظريات التي تقبل "التبريد الكوني" كاستنتاج نهائي. من ناحية، ومن ناحية أخرى تم اقتراح أن أحد الحلول الممكنة لمفارقة فيرمي هو أن الذكاءات أو الحضارات الفضائية الذكية خارج كوكب الأرض (ETIs) نائمة وتنتظر الكون حتى يتحسن (فرضية aestivation).

استنادًا جزئيًا إلى الديناميكا الحرارية للحوسبة (مبدأ لانداور)، تؤكد الحجة أنه مع برودة الكون، ستكون الأنواع المتقدمة قادرة على ضغط المزيد من البنى التحتية الضخمة. أيضًا، إذا ازدادت حرارة الكون بمرور الوقت، فهل يعني ذلك أن ظهور الحياة سيصبح أقل احتمالًا بمرور الوقت بسبب زيادة الإشعاع الكوني؟ بافتراض عدم وجود آلية للحفاظ على توازن حراري معين، فهل يعني ذلك أن الكون لن ينتهي ببرودة كبيرة، ولكن بنيران كبيرة؟

وفقًا لبحث جديد من مركز علم الكونيات وفيزياء الجسيمات الفلكية (CCAPP) في جامعة ولاية أوهايو، يبدو أن الكون يزداد سخونة وسخونة بمرور الوقت. بعد التحقيق في التاريخ الحراري للكون على مدى العشرة مليارات سنة الماضية، خلص الفريق إلى أن متوسط درجة حرارة الغاز الكوني قد زاد أكثر من 10 مرات ووصل إلى حوالي 2.2 مليون كلفن (~ 2.2 مليون كلفن). درجة مئوية) اليوم.

نُشرت الدراسة التي تصف النتائج التي توصلوا إليها في مجلة الفيزياء الفلكية. قام الفريق بفحص البيانات الحرارية حول بنية الكون واسعة النطاق (LSS). يشير هذا إلى نماذج المجرات والمادة على نطاق واسع.

ج- ظهور النسبية العامة:

بحلول عام 1911، كان أينشتاين قد فهم المبادئ الرئيسية لما يمكن أن تكون عليه نظريته في النسبية العامة:

- مبدأ النسبية كما تمت صياغته في النسبية الخاصة هو مبدأ عالمي، وهو ينطبق على جميع المراقبين بالقصور الذاتي (محليًا أم لا)، وجميعهم في حالة سقوط حر.

- إذا كان هناك مصدر لحقل الجاذبية، يكون الزمكان منحنيًا، ومهما كان هذا الانحناء، فإن المراقبين بالقصور الذاتي يتبعون "الجيوديسيا من النوع الزمني" لهذا الزمكان 5؛

- التسارع محليًا دائمًا ما يعادل وجود مجال الجاذبية.

لذلك كانت المهام الوحيدة المتبقية له هي صياغة كل هذا رياضيًا واكتشاف كيف يثني مصدر الجاذبية بدقة الزمكان، وهو ما يرقى إلى إيجاد المعادلة الرمزية التي سبق ذكرها:

الاختلاف النسبي في مجال الجاذبية النسبية = كثافة الكتلة والطاقة النسبية.

طلب أينشتاين، الذي كان يجهل هندسة المساحات المنحنية في ذلك الوقت، المساعدة من صديقه، عالم الرياضيات الألماني مارسيل غروسمان. هذا الأخير، الذي لم يكن في البداية خبيرًا في هذا المجال المحدد أيضًا، انغمس في أعمال ريمان وعمل "خلفائه"، عالم الرياضيات الألماني إلوين برونو كريستوفيل، وكذلك الإيطاليين غريغوريو ريتشي كورباسترو وتوليو ليفي سيفيتا. لن يتم تفصيل الأدلة الخاطئة المتنوعة التي اتبعها آينشتاين وغروسمان، والأمر المهم هو أنهما في عام 1913 قاما بالتوقيع على أول مقال تم فيه وصف الجاذبية باستخدام "موتر متري"، وهو موتر مشتق بشكل طبيعي من الهندسة الريمانية والتي تميز المساحات المنحنية. هذا الموتر، الذي سيتم وصفه بإيجاز شديد، يتكون من 10 معاملات مستقلة (إنه متماثل)، و10 "جهود جاذبية"، ويجعل من الممكن التعميم على الفضاء المنحني مضروبًا في فكرة المسافة بين الزمكان التي قدمها مينكوفسكي. كل من معاملات هذا الموتر اعتمادًا على الموضع في الزمكان، والفكرة هي استبدال التعريف العام والمسطّح لـمينكوفسكي Minkowski بتعريف محلي ومنحني. أولاً، يجب إعادة كتابة معادلة مينكوفسكي مع إعطاء المسافة التي تفصل بين حدثين، مع إحداثيات (x1 ، t1) و (x2 ، t2) ، S² = c² (t2-t1) ² - (x2-x1) ² ، في حالة اقتراب هذين الحدثين ، مما يجعل من الممكن الوصول إلى التعريف المحلي ds² = c² dt² - dx² ، حيث يكون للأحداث إحداثيات (x1، t1) و (x1 + dx، t1 + dt) ، مربع المسافة الآن ds². هاتان المعادلتان متكافئتان تمامًا، لكن الثانية محلية، بينما كانت الأولى عالمية أو شاملة. ومع ذلك، كما قيل سابقًا، تستدعي الهندسة الريمانية بالضرورة المفاهيم المحلية، فمساحات ريمان ليست بالضرورة موحدة. وبالتالي، بدءًا من هذه المسافة المكانية والزمانية الثانية، المحلية ولكن المسطحة، فإننا نقدم بشكل طبيعي الانحناء المحلي من خلال الكتابة أنه يجب تحديد المسافة بشكل عام من خلال ds² = gtt dt² + gxx dx² + 2 gtx dx dt ، حيث المعامِلات g هي معاملات المقياس ، والتي سوف نتحقق من أنها بالفعل 10 إذا كتبنا جميع المصطلحات الممكنة التي تتضمن إحداثيين. في هذا التعبير المحلي، ينتج انحناء الزمكان من حقيقة أن هذه المعاملات (التي تساوي 1 أو -1 أو 0 في حالة الزمكان لمينكوفسكي) ليست ثابتة، ولكنها تعتمد على الإحداثيات ( s ، d) من النقطة المدروسة. ومع ذلك، نلاحظ أن عدم ثبات المقياس هو شرط ضروري غير كافٍ لوجود انحناء (راجع حالة المستوى الإقليدي الموصوف في الإحداثيات القطبية).

أما بالنسبة لمبدأ النسبية المعمم، فهو ينص ببساطة على أن التغييرات في أنظمة الإحداثيات التي تربط الأطر المرجعية التي تتخذ فيها قوانين الفيزياء نفس الشكل ليست فقط تلك المرتبطة بتحولات لورينتز والتي تترك المسافة S² دون تغيير.، ولكن بشكل عام، جميع التغييرات المحلية التي تعتبر ds² كمية ثابتة. نبيّن أن هذا الثبات يشير إلى مخاريط الضوء، حتى لو لم تعد الأخيرة متوازية بسبب انحناء الزمكان (انظر الشكل التالي). يوضح هذا الثبات لمخاريط الضوء مرة أخرى أهمية هذه الأشياء الهندسية ويؤكد حقيقة أنه حتى في النسبية العامة، فإن سرعة الضوء ثابتة ولها نفس القيمة لجميع المراقبين، على الرغم مما نعنيه بهذا القول احيانا. علاوة على ذلك، فإن حقيقة أنه يجب علينا تحديد ds² محليًا تظل متوافقة أيضًا مع وجود وقت مناسب محدد على طول خطوط الأكوان من نوع الوقت (= الجيوديسية التي ds²> 0) بواسطة العلاقة "dτ = ds / c" ، ويجعل المرء للجيوديسيا نفس تصنيف خطوط الأكوان، ويفصل بينها في "نوع الزمن" و "نوع الفضاء" و "نوع الضوء" (هذه الأخيرة هي بعض وتسمى أيضًا "الجيوديسيا الفارغة").

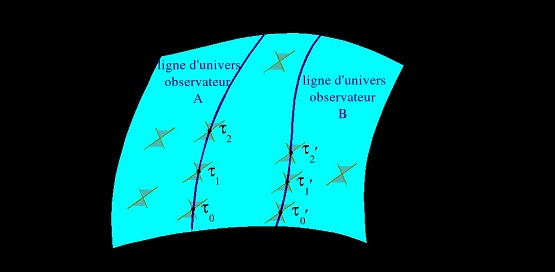
توضيح الزمكان للنسبية العامة (للمقارنة (على سبيل المثال لأرقام مماثلة في الزمكان لمينكوفسكي) حيث تظهر خطوط الكون لمراقبين وبعض مخاريط الضوء التي "يعترضونها". تدل مسلمة النسبية المعممة على أن هذه الأقماع هي نفسها لجميع المراقبين، حتى لو كان انحناء الزمكان يعني أنها ليست بالضرورة "موازية".

ولتطبيق مبدأ الثبات المحلي هذا وبناء نظرية كاملة، من الضروري تقديم شكليات رياضياتية كاملة والتي قد تبدو مجردة تمامًا لأولئك الذين لا يتقنونها، وهذا هو السبب في أن فهم ما سبق لم يكن كافياً لأينشتاين وغروسمان للعمل على النظرية بأكملها. مع ذلك، من المهم التأكيد هنا على أن ما ورد أعلاه يصف (تقريبًا) كل ما نحتاج إلى معرفته لتوسيع مبدأ النسبية الذي صاغه أينشتاين في نظريته النسبية الخاصة ليشمل جميع المراقبين، حتى مع التسارع. إن الثبات المحلي والعامة (ليس فقط فيما يتعلق بالتحولات الخطية للإحداثيات) لـ ds² (مع شكليات الهندسة الريمانية المرتبطة) كافٍ لتطبيق مبدأ النسبية المعمم في حالة الزمكان حيث الجاذبية لن تكون موجودة، على سبيل المثال الزمكان المينكوفسكي. ومع ذلك، لم يكن هذا هو الأهم أو الأكثر إشكالية بالنسبة لأينشتاين وغروسمان، فالنسبية العامة تذهب إلى أبعد من ذلك لأنها غير راضية عن كونها تعميمًا لمبدأ النسبية لجميع المراقبين الأحرار: إنها أيضًا نظرية الجاذبية النسبية. ما استغرقه أينشتاين وغروسمان أطول وقت هو الحصول على ما يعادل معادلة نيوتن التي تصف مجال الجاذبية الناتج عن توزيع كتلة معين، أي المعادلة الرمزية التي سبق ذكرها. كان لديهم معيار اختيار قوي جدًا: تم تطبيقه على حالة حقول الجاذبية الضعيفة، وكان على نظرية الجاذبية الجديدة أن تعطي نظرية نيوتن مرة أخرى.

ومع ذلك، مع إدخال المقياس الزماني المكاني المحلي كتعميم نسبي لإمكانات الجاذبية، قد يعتقد المرء أن شروط المعادلة الرمزية قد تم تعريفها بالكامل تقريبًا، حيث تقرر أيضًا أن "كثافة الكتلة النسبية- سوف يكون موتر طاقة النبض المذكور سابقًا. في الواقع، ظل "التباين النسبي" فقط في مجال الجاذبية مجهولًا، لكن تحديد هذا المشغل الرياضياتي استغرق عدة سنوات لأينشتاين (تخلى غروسمان عن التعاون في منتصف الطريق)، الذي لم يحصل على نسخته النهائية من "معادلات أينشتاين" حتى نهاية عام 1915. بعد فترة وجيزة، اقترح عالم الرياضيات الألماني ديفيد هيلبرت، الذي ناقش معه أينشتاين بإسهاب أفكاره ومشكلاته الرياضياتية، علاوة على ذلك، اشتقاقًا آخر لهذه المعادلات يستند إلى مبدأ متغير وما يعرف الآن باسم "أينشتاين-هيلبرت لاغرانج". وحتى إذا جاء التحقق الحقيقي للنظرية من خلال التجربة سريعًا، فقد اقتنع أينشتاين، منذ إرسال مقالته (25 نوفمبر 1915)، بـ "صحة" معادلاته من خلال الحساب الذي كان لديه. حقيقة تتعلق بما يعتبر أحد الاختبارات الأساسية الثلاثة للنسبية العامة مسار مدار عطارد وحضيضه.

معادلات أينشتاين للنسبية العامة مع الثابت الكوني (لامدا على اليمين). على اليسار، موتر أينشتاين G الذي يصف هندسة الزمكان، على اليمين يظهر موتر زخم الطاقة T الذي يصف محتوى المادة. في عبارة ويلر "الزمكان يخبر المادة كيف يجب أن تتحرك والمادة تخبر الزمكان كيف يجب أن ينحني".

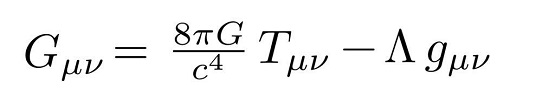
د- الاختبارات الأساسية الثلاثة:

قرابة منتصف القرن التاسع عشر، قام عالم الفلك الفرنسي أوربان جوزيف لو فيرييه بقياس إزاحة الحضيض (نقطة في مدار كوكب يقع على مسافة لا تقل عن الشمس) من عطارد بمرور الزمن. كما تنبأت نظرية نيوتن، كان هناك تقدم في الحضيض الشمسي بسبب "اضطرابات الجاذبية" الناجمة عن التجاذب الذي تمارسه أجسام أخرى في النظام الشمسي على كوكب عطارد. ومع ذلك، في حين أن نظرية نيوتن المرتبطة بالكواكب المعروفة تنبأت بحدوث تحول قدره 529 ثانية قوسية في القرن، أعطت الملاحظة قيمة قدرها 572. كانت الملاحظات موثوقة، لذلك في السنوات التي تلت التفسيرات الفيزيائية الفلكية المختلفة، تم النظر فيها من أجل 43 ثانية من القوس الفائض، تتراوح هذه الافتراضات من وجود فولكان بركان (جسم أقرب إلى الشمس من عطارد والذي ادعى البعض أنه يلاحظ، أحيانًا في عدة أماكن في نفس الوقت)، إلى أن تسطيح الشمس (انظر على سبيل المثال كتاب آيزنشتاد). ومع ذلك، لم يتم التحقق من أي من الأفكار التي تم النظر فيها بوسائل أخرى. إن الملاحظة و / أو جعلت من الممكن تفسير هذه الفجوة "الكبيرة" بين النظرية والملاحظة، وظل اللغز دون حل في عام 1915.

بسرعة كبيرة، وحتى قبل الحصول على النسخة النهائية من نظريته الجديدة في الجاذبية، كان لدى أينشتاين فكرة أنه بمجرد حصوله على نظرية قادرة على رد الجميل لنيوتن، كان اختبار عباد آخر هو حساب l الحضيض المتقدم للزئبق. في الواقع، هذا الأخير هو الكوكب الأقرب إلى الشمس، فهو يقع في المنطقة التي يكون فيها مجال الجاذبية أقوى، وبالتالي من المرجح أن يشهد على تعديلات قانون الجاذبية مقارنة بقانون نيوتن. والآن، حتى لو، خلال السنوات الطويلة التي سعى فيها مع غروسمان للحصول على نظريته الجديدة، اختبر أينشتاين جميع المرشحين دون جدوى، وفي نوفمبر 1915 أجرى حسابًا ذهب إلى حد جعله يعاني من خفقان القلب (وفقًا لنظريته الخاصة)): تنبأت نظريته بالنتيجة الصحيحة تمامًا.

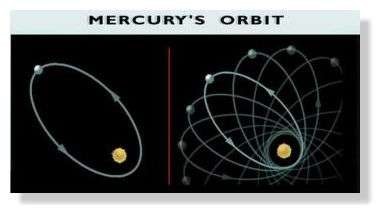
رسم توضيحي لظاهرة الحضيض التقدمي لكوكب معزول يدور حول نجم. هذه الظاهرة ناتجة عن تصحيح تم إجراؤه على الجاذبية النيوتونية بواسطة نظرية أينشتاين. إن التأثيرات مبالغ فيها للغاية من أجل جعل التحول مرئيًا مع عدد قليل من الثورات.

من المثير للاهتمام أيضًا أن نذكر أن هذه الظاهرة موجودة أيضًا بالنسبة للأجسام الأخرى في النظام الشمسي، ولكن تأثيرها أضعف بكثير من تأثير عطارد بسبب المسافة الأكبر من الشمس. على سبيل المثال، بالنسبة إلى كوكب الزهرة، ثاني أقرب كوكب، فإن الفرق بين النظرية النيوتونية والنسبية هو 8.6 ثانية قوسية فقط لكل قرن، وهي قيمة تنخفض إلى 1.35 بالنسبة للمريخ. ولكن على الرغم من ضعف القيمة الأخيرة، منذ أن "هبطت" مجسات الفايكنج على سطح المريخ في عام 1976، فإن رصدها باستخدام موجات الراديو، لعدة سنوات، سمح للمريخ بأن يصبح الجسم الذي يتقدم تم قياس الحضيض بأقصى دقة، في توافق تام مع تنبؤات النسبية العامة.

من ناحية أخرى، في مقال عام 1915 حيث تم تقديم النسخة النهائية من نظريته، صحح أينشتاين النتيجة التي أعلن عنها في عام 1911 فيما يتعلق بالاختبار الأساسي الثاني للنسبية العامة: انحراف مسار ضوء قريب من الشمس. لقد أجرى بالفعل أول عملية حسابية بنسخة خاطئة من نظريته وكانت النتيجة التي تم التنبؤ بها بعد ذلك خاطئة بمعامل قدره 2. ومع ذلك، على عكس تقدم حضيض عطارد الذي كان معروفًا قبل نظرية أينشتاين بفترة طويلة، كان هذا التأثير الثاني تنبؤًا بالنسبية العامة، وكان من الممكن أن يتم التحقق منها قبل عام 1919 دون "مشاكل" مختلفة مثل الحرب العالمية الأولى (لمزيد من التفاصيل، انظر كتاب آيزنشتاين). على أي حال ، في عام 1919 ، بالاستفادة من الكسوف الكلي للشمس (مما جعل من الممكن مراقبة النجوم التي يمكن رؤيتها بالقرب من القرص الشمسي دون أن تغرق في وضوح الأخير) ، رحلتان استكشافيتان أكدتا الفرق البريطانية بقيادة آرثر إدينجتون توقع أينشتاين ، والقيم المقاسة ، بالقرب من الدائرة الشمسية ، لزاوية الانحراف من قبل فريقين مستقلين (1.98 +/- 0.12 و 1.61 +/- 0 ، 3 ثوان قوسية) تتفق جيدًا مع القيمة المتوقعة البالغة 1.75 ثانية قوسية ، على عكس القيمة الأقل بكثير التي يمكن توقعها في إطار نيوتن (تم قياس الانحراف الأصغر أيضًا لـ المزيد من النجوم البعيدة ، مرة أخرى وفقًا للتنبؤات). علاوة على ذلك، تم اختبار هذه النتيجة مرة أخرى بعد ذلك بوقت قصير لصالح كسوف كلي آخر للشمس في عام 1922. ولكن منذ عام 1919، بين عشية وضحاها، اكتسب أينشتاين شهرة دولية بين عامة الناس، الغالبية العظمى من المجلات التي استغلت الفرصة ، بعد فترة وجيزة من نهاية الحرب ، لإظهار كيف أثبت عالم بريطاني أن ألمانيًا ، يتحدى كل ما يبدو أنه حدس طبيعي جدًا حول المكان والزمان ، كان محقًا في مواجهة نيوتن العظيم.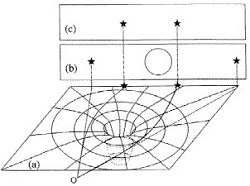

رسم توضيحي لظاهرة انحراف الضوء عندما يمر بالقرب من جسم ضخم ينطوي، وفقًا لتفسير أينشتاين، على تشوه أكبر في الزمكان. (أ): تمثيل تخطيطي للانحناء؛ (ب) المواضع التي لوحظت خلال الكسوف؛ (ج) المواقف الحقيقية التي يمكن التحقق منها بسهولة في الليل. الآثار مبالغ فيها لجعل الفرق ومبدأ التجربة أكثر وضوحا.

يتعلق "الاختبار الكلاسيكي" الثالث للنسبية العامة بـ "تأثير أينشتاين"، وهو التغير في التردد الذي يمر به الضوء أثناء مروره من مكان يكون فيه مجال الجاذبية له قيمة معينة إلى مكان آخر حيث القيمة مختلفة. في الواقع، هذا الاختبار، الذي يعادل مقياس تأثير مجال الجاذبية إذا كان الوقت أطول في إدراكه من السابق، حتى لو مرت به النسبية العامة اليوم بنجاح كبير في ظل ظروف عديدة. وهكذا، تم إجراء التحقق الأول في عام 1960 من قبل الأمريكيين روبرت في باوند وغلين إيه ريبكا في مجال الجاذبية الأرضية مع اختلاف في مجال الجاذبية يأتي فقط من اختلاف ارتفاع يبلغ 22 مترًا بين مصدر الضوء والمتلقي. على الرغم من الاختلاف النسبي الضئيل جدًا في الطول الموجي الذي كانوا يأملون في قياسه في ظل هذه الظروف (جزء واحد لكل مليون مليار، أو 10-15)، فقد نجحوا بفضل استخدام واحدة من أشهر "الساعات الطبيعية" الأكثر دقة في العالم: إزالة الإثارة الذرية التي تؤدي إلى إنتاج فوتون من طاقة محددة بدقة، من خلال التأثير الذي اكتشفه رودولف موسباور في عام 1957. كما ستوضح بعض التفاصيل التاريخية في الفقرات التالية حول الاختبارات الأكثر حداثة في النسبية العامة، تزامنت تجربة باوند وريبكا مع الوقت الذي بدأت فيه النسبية العامة، بفضل تطور الفيزياء الفلكية عالية الطاقة، في أن تصبح موضوعًا جديرًا باهتمام علماء الفيزياء النظرية، الذين سبق أن فضلوا فيزياء الكموم والديناميكا الكهربائية الكمومية.

كثيرًا ما كرر أينشتاين أنه عندما كان صغيرًا جدًا، حاول أن يتخيل كيف سيبدو الكون لعالم "راكبًا" على موجة ضوئية وأن هذا ساعده على تصور نظريته النسبية.

2 على عكس ما نسمعه أحيانًا يقول الناس، يمكن لنظرية الجاذبية لنيوتن أن تستوعب بشكل جيد فعل الجاذبية على الضوء، وذلك بفضل الرؤية الجسدية لهذه التي كان نيوتن يمتلكها. ومع ذلك، في سياق النسبية العامة، ليس للجاذبية نفس التأثير بالضبط على الضوء وعلى الأجسام الضخمة، بسبب الكتلة الصفرية للفوتونات. بالإضافة إلى ذلك، يجب ألا يكون الضوء الموجي قادرًا على "انحرافه" بواسطة مجال الجاذبية النيوتونية، بينما يمكن أن يكون كذلك في حالة النسبية العامة.

3 يعرّف إقليدس سابقًا خطين متوازيين على أنهما "خطان، مضمنان في نفس المستوى وممتدان إلى أجل غير مسمى، ليس لهما نقطة تقاطع".

4 هذه النقطة تستحق مناقشة أطول مما هو ممكن ومرغوب فيه هنا. انظر، على سبيل المثال، Science and the Hypothesis، Poincaré (1902).

سيتم تعريف تعبير "الجيوديسية الشبيهة بالزمن" لاحقًا، ولكنه مجرد تعميم لـ "خط الكون الشبيه بالزمن" الذي واجهته سابقًا في الزمكان عند مينكوفسكي. علاوة على ذلك، من المثير للاهتمام أن نلاحظ أنه بعد سنوات قليلة من الصياغة النهائية لنظريته، أوضح أينشتاين، جنبًا إلى جنب مع ليوبولد إنفيلد وبانيش هوفمان، أن فرضية الحركة الجيوديسية لم تكن ضرورية: الحركة الجيوديسية لـ الجسيم النقطي هو نتيجة مباشرة للمعادلات التي تعطي مجال الجاذبية وفقًا للمصدر الذي يخلقه.

6 بشكل أكثر دقة، كان الأمر يتعلق بتحديد نتيجة هذا العامل المطبق على موتر متري g، وهو "موتر أينشتاين" ويتضمن كمكون أساسي موتر انحناء ريمان-كريستوفل.

7 على الرغم من أنه يُسمع أحيانًا أن هيلبرت قد اكتشف هذه المعادلات قبل أينشتاين (التي لم يدعها هيلبرت مطلقًا)، إلا أن هذا خطأ يتعلق بحقيقة أن التاريخ الذي أرسل فيه هيلبرت النسخة الأولى من مقالته تسبق تلك التي أرسلها أينشتاين. ومع ذلك، فإن النسخة الأولى من مقالة هيلبرت لا تحتوي على المعادلات، والنسخة النهائية تعطيهم ملاحظة مفادها أنهم في اتفاق جيد مع تلك التي اكتشفها أينشتاين مؤخرًا.

8 من المهم أن نلاحظ أنه منذ ذلك الحين تم التحقق من انحراف الضوء عن طريق مجال الجاذبية في بيئات تجريبية أخرى بدقة أفضل بكثير.

د. جواد بشارة